blog informativo

Más allá del kriging: el rol de las simulaciones condicionales en la evaluación de recursos

En los últimos años, las simulaciones condicionales han adquirido un lugar cada vez más importante en la evaluación de Recursos Minerales. Hoy son requeridas con mayor frecuencia en proyectos y en minas en operación, debido a sus múltiples usos. Sin embargo, su alta complejidad hace que aún no sean utilizadas de manera transversal en la industria. En el siguiente blog, aprenderemos qué son, qué las diferencia de los estimadores lineales tradicionales y algunos de sus usos en casos reales trabajados en GeoEstima.

¿Qué son las simulaciones geoestadísticas?

Son una aplicación de la simulación de Monte Carlo a variables regionalizadas que permiten cuantificar la incertidumbre de los modelos. Las técnicas de simulación geoestadísticas generan un grupo de realizaciones o realidades con igual probabilidad de ocurrencia. Si existe una mayor variabilidad en los datos o existen menos datos para generar el modelo, las realizaciones tendrán un mayor grado de diferencia entre ellas (Abzalov, 2016).

Dependiendo de su aplicación, pueden ser usadas en variables categóricas (litologías, zonas minerales, alteraciones) o en variables continuas (leyes, densidad, recuperaciones) (Rossi & Deutsch, 2014; Chiles & Delfiner, 2012). Normalmente, utilizamos simulaciones condicionales, que restituyen los valores medidos en los sitios con datos. Por lo tanto, estos sitios con información no tendrán incertidumbre (Emery, 2015).

Los modelos generados tienen la particularidad de reproducir la distribución o histograma de los datos (proporción de valores altos, bajos, media y varianza) y el variograma (continuidad espacial, anisotropías y efecto pepa) (Rossi & Deutsch, 2014). La idea de las simulaciones condicionales es construir una representación del fenómeno que sea consistente con los datos y que reproduzca las fluctuaciones locales: no es la realidad, pero si una posible versión de ella (Chiles & Delfiner, 2012).

Entre algunas consideraciones prácticas que se deben tener en cuenta está la necesidad de calcular los pesos de desagrupamiento de las muestras para poder tener la distribución representativa del fenómeno y no una distribución sesgada por el muestreo preferencial. Otro factor importante es la definición de dominios, ya que las simulaciones condicionales son sensibles a la no estacionaridad. Para utilizar simulaciones, es necesario transformar los datos al espacio gaussiano previamente (media cero, varianza uno), lo que se hace mediante una función llamada anamorfosis. Finalmente, las simulaciones representan las leyes o valores en soporte puntual y sus resultados deben ser rebloqueados promediados al soporte de interés (SMU).

Existen diversos algoritmos de simulaciones geoestadísticas disponibles en muchos de los softwares comerciales. Algunas técnicas de simulaciones de variables continuas son el algoritmo secuencial gaussiano (SGS) o el algoritmo de bandas rotantes (TB). Del mismo modo, algunos de los algoritmos populares para simular variables categóricas son la simulación secuencial de indicadores (SIS), la simulación multipunto (MPS) o la simulación plurigaussiana jerárquica truncada (HTPG).

Estimación vs simulación

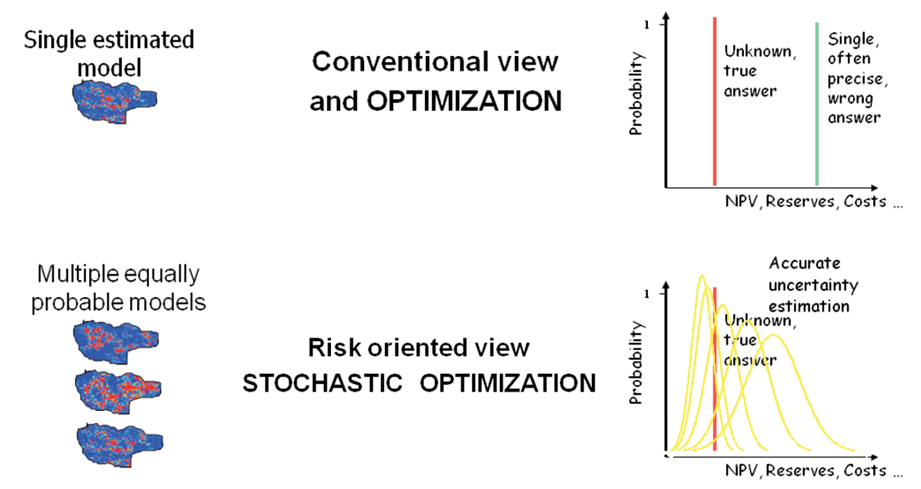
Las estimaciones entregan un valor que en promedio se acerca al de la realidad desconocida. Es una combinación lineal de los datos disponibles, insesgada, tiene el menor error cuadrático e inevitablemente presenta suavizamiento (mínimos mayores y máximos menores a los datos). Las estimaciones entregarán el valor esperado.

Las simulaciones, por otro lado, son modelos no lineales, reproducen la variabilidad de los datos, lo que implica que preservan los valores extremos de los datos (no suavizan). Las simulaciones entregan un grupo de valores a cada punto, lo que permite cuantificar la incertidumbre. Las simulaciones van a reproducir de forma correcta la proporción de valores altos y bajos.

Tabla 1: Resumen comparativa estimaciones y simulaciones

En la Figura 1 se observa cómo el modelo estimado al ser suavizado muestra valores mínimos más altos y valores máximos más bajos, mientras que las simulaciones al ser no suavizadas reproducen mejor los valores bajos y altos. Además, se observa como la estimación es un solo modelo, mientras que las simulaciones son N modelos con igual probabilidad de ocurrencia.

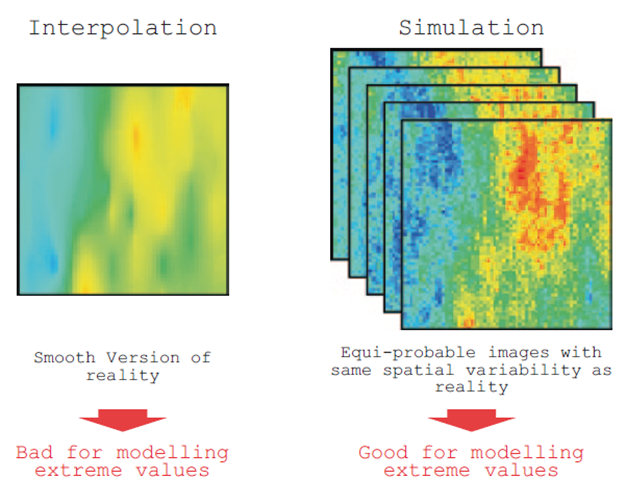
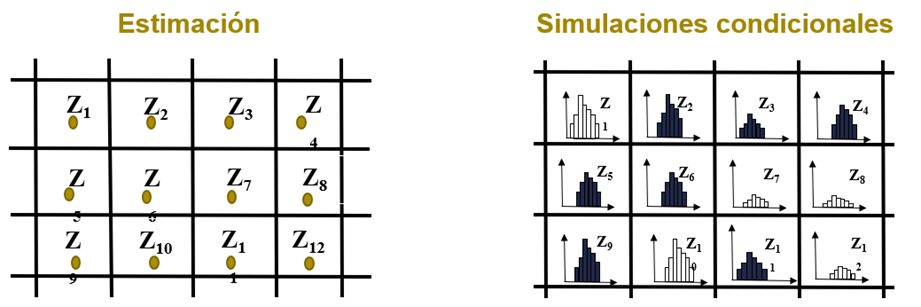
Figura 1: Estimación vs simulación (Rossi & Deutsch, 2014)

Como se mencionó, las estimaciones entregan un único valor en cada bloque del modelo, mientras que las simulaciones al ser N modelos, entregan una distribución de valores para cada bloque (Figura 2).

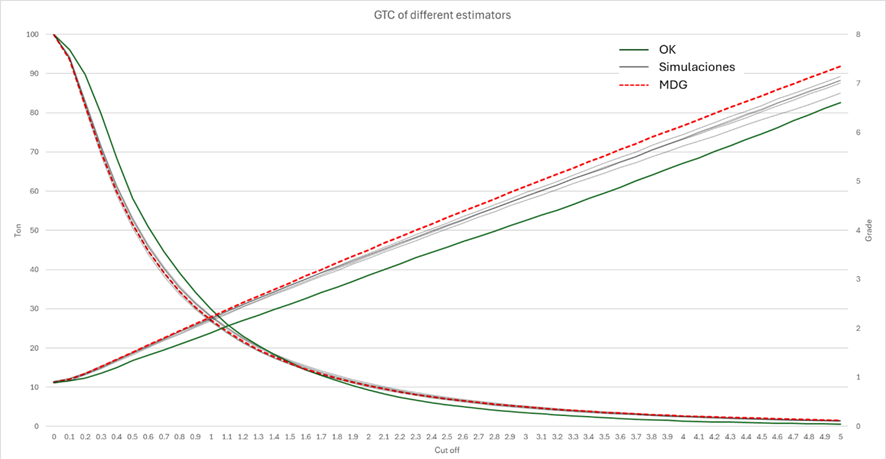
Figura 2: Estimación vs simulación en cada bloque

Si utilizamos el modelo de discreto gaussiano como referencia, podemos observar la diferencia entre un modelo estimado por kriging y un modelo simulado en términos de curva tonelaje ley: el kriging al suavizar reporta más tonelaje de baja ley y menos tonelaje de alta ley, mientras que las simulaciones no tienen estas desviaciones. Del mismo modo, el kriging siempre reporta una menor ley media a ley de corte mayor a cero (solo es insesgado a ley de corte 0) a diferencia de las simulaciones condicionales. Para esta comparación, las simulaciones puntuales fueron promediadas al soporte de SMU, mismo del kriging.

Figura 3: Curva tonelaje ley modelo tradicional vs simulaciones

¿Por qué usar simulaciones?

Debido al alto riesgo que constituye cualquier proyecto minero, la incertidumbre y el consiguiente riesgo debe ser cuantificado para una mejor toma de decisiones.

La ventaja de las simulaciones frente a las estimaciones tradicionales es que a partir de ellas podemos generar modelos de incertidumbre a partir del cual se pueden realizar diversos tipos de estudios: análisis de riesgos, cuantificación de la incertidumbre tanto de geología como de leyes, definición de categoría de recursos, estudio de potencial de mineralización y estudios de optimización de espaciamiento de sondajes y, recientemente, para planificación estocástica.

¿Cómo integrarlas de forma correcta al flujo de trabajo?

Si bien las simulaciones se utilizan normalmente para cuantificar la incertidumbre de las leyes, limitar el estudio de simulaciones solo a esto es un error, debido a que la idea es siempre integrar la mayor cantidad de fuentes de incertidumbre del modelo para no tener solo una mirada parcial.

Cuando sea posible, se recomienda cuantificar la variabilidad en cada etapa del estudio de recursos, siguiendo un flujo de trabajo jerárquico y una configuración de una-a-una realización. La Figura 4 muestra de forma esquemática la integración de la incertidumbre en las distintas etapas del modelo siguiendo la configuración una-a-una y transfiriendo la incertidumbre en cada etapa (Deutsch, 2018; Deutsch, 2021).

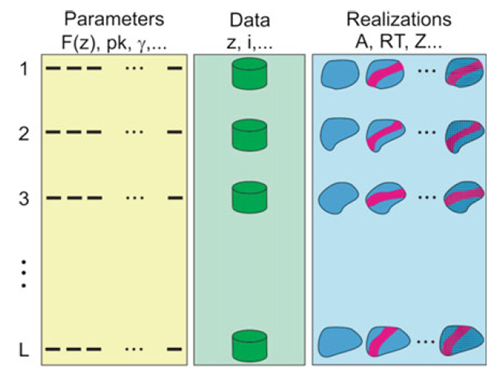
Figura 4: Simulaciones en cada etapa del flujo de trabajo (Deutsch, 2021)

Incertidumbre de datos: en caso de estudio multivariables, si se tienen bases de datos heterotópicas, se recomienda imputar los datos faltantes generando realizaciones de estos e integrando estas realidades una a una al estudio.
Incertidumbre de parámetros: es posible realizar Bootstrap espacial para cuantificar la incertidumbre en el histograma de los datos.
Incertidumbre en la geología: la geología tiene una variabilidad intrínseca que impactará directamente en los volúmenes mineralizados y en el tonelaje que se reporte, por lo que cuantificar la variabilidad de los contactos es crucial para entender la variabilidad total del fenómeno que se está modelando.
Incertidumbre de las leyes: es la etapa del flujo que normalmente se realiza, es la cuantificación de la incertidumbre de las leyes de interés (minerales económicos y contaminantes cuando corresponda). En caso de ser un estudio multivariable, se debe decidir entre hacer co-simulaciones o simular factores independientes (transformaciones como PPMT, projetion pursuit multivariat transformation o MAF, Min-max autocorrelated factor), para que las simulaciones resultantes mantengan las correlaciones de los datos y otras estructuras complejas en los datos debido a heteroscedasticidad o no linealidades.
De esta forma, al integrar en cada paso sucesivo la incertidumbre, el resultado final será un reflejo mucho más fiel de la variabilidad total del proceso y el posterior análisis que se realice será mucho más robusto.

Ejemplos de usos

A continuación, presentaremos casos prácticos de la gran minería en los que las simulaciones entregaron buenos resultados y llevaron a una mejor toma de decisiones.

Cuantificación de la incertidumbre geológica

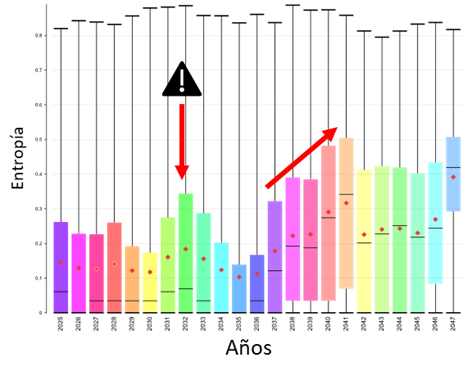
A partir de las simulaciones condicionales, se calculó la variable entropía, la cual cuantifica de forma resumida la incertidumbre del modelo geológico. A partir de este, es posible definir zona en que el modelo sea más incierto y que, por lo tanto, requiera una mayor cantidad de información (sondajes) para ser correctamente caracterizado (Figura 5). Esto puede ayudar a la planificación de nuevas perforaciones (Figura 6) o a tomar medidas de mitigación, como mezcla de materiales de diferentes zonas o ajustar el plan para que no vayan a planta distintos frentes con alta entropía.

Figura 5: Zonas de alta entropía en el plan minero

Figura 6: Recomendación de nuevos sondajes (en negro) en zoans de alta incertidumbre geológica

Estudios de malla para la definición de categoría de recursos

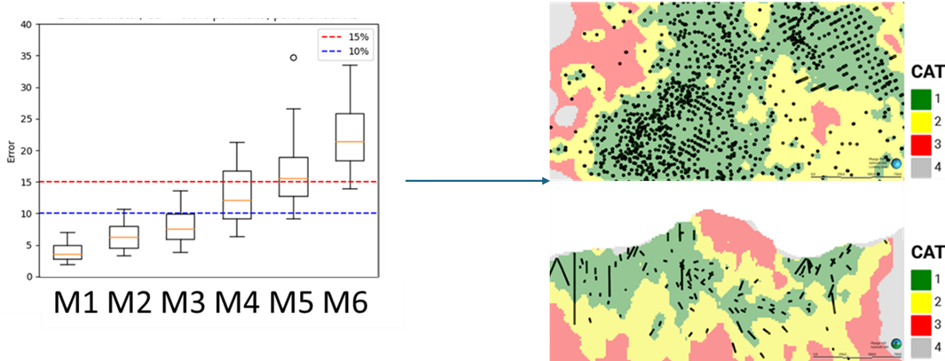
A partir de un estudio de simulación, muestreo artificial y re-simulación es posible cuantificar la relación entre espaciamiento de sondajes e incertidumbre, es decir, podemos medir cuánto disminuirá la variabilidad del yacimiento con la llegada de nueva información. Si esto lo relacionamos con un error tolerado y un nivel de confianza, podemos definir las mallas de sondajes necesarias para las categorías medido e indicado. La ventaja de este estudio con respecto a otras herramientas de categorización radica en que la incertidumbre es medida directamente y se integra la variabilidad de la geología como de las leyes. Además, permite medir el error sobre una ley de corte.

Figura 7: Incertidumbre vs espaciamiento y categorización de recursos

Análisis de riesgo para corto plazo

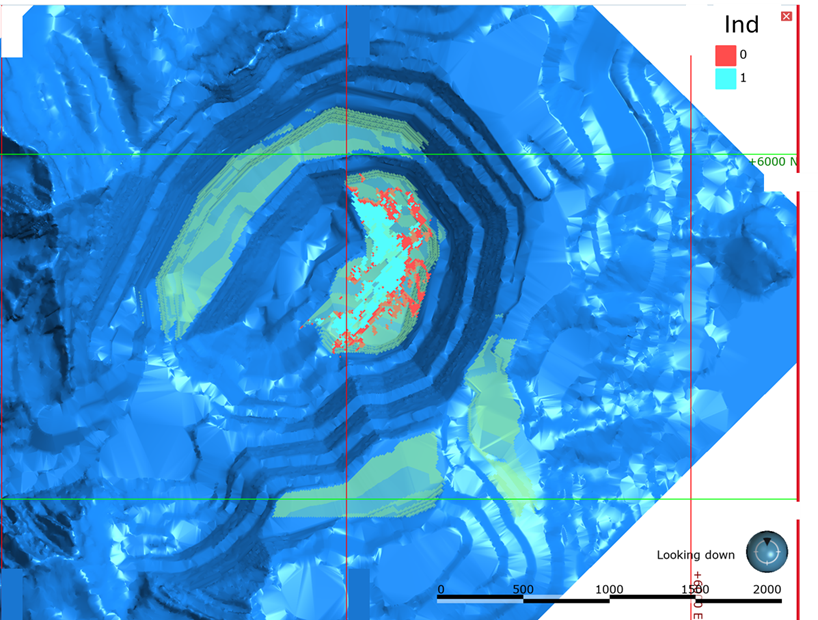
A partir del modelo simulado, se generó un indicador de confianza del 90% de ser roca mineralizada y de sobrepasar la ley de corte operacional. Este indicador se cruzó con el modelo de recursos oficial y se identificaron bloques que en el modelo determinístico eran roca mineralizada y superaban la ley de corte, pero que las simulaciones indicaban una baja probabilidad de serlo. Al revisar este indicador con las reconciliaciones se observó una correlación entre el indicador y resultados deficientes del modelo de recursos oficial. De este modo, el indicador fue utilizado por el equipo de corto plazo para identificar fases y bancos prontos a explotar con una alta probabilidad de error (bloques en rojo Figura 8).

Figura 8: Indicador, en rojo, zonas de alto riesgo (baja probabilidad de ser lo planificado)

Planificación estocástica

Los modelos simulados de geología y leyes pueden ser utilizados como input para algoritmos de planificación estocástica. Recientemente, GeoEstima finalizó un modelo para un yacimiento world-class de Cu en que se simularon las zonas minerales, las litologías y las leyes de Cu, Cus y Mo. En conjunto, estos 100 modelos serán utilizados para integrar la incertidumbre del depósito al diseño de la mina, plan de producción y en la evaluación económica de proyectos mineros y operaciones. Los flujos estocásticos incrementan hasta en un 15% el tonelaje total cuando se comparan a la planificación tradicional. Además, se ha demostrado un incremente de hasta un 10% del VAN entre la planificación estocástica y tradicional (Dimitrakopoulos, 2018).

Figura 9: Enfoque tradicional vs estocástico (modificado de Dimitrakopoulos, 2018)

Las simulaciones condicionales están revolucionando la forma en que entendemos la incertidumbre en minería. ¿Has trabajado con ellas? ¿Quieres saber cómo pueden ayudarte a tomar mejores decisiones y reducir riesgos en tus proyectos?

Referencias

Abzalov, M. (2016). Applied mining geology (Vol. 12).
Chiles, J.-P., & Delfiner, P. (2012). Geostatistics : Modeling Spatial Uncertainty. John Wiley & Sons.
Deutsch, C. V. (2018). All Realizations All the Time. In Handbook of Mathematical Geosciences (pp. 131–142). Springer International Publishing. https://doi.org/10.1007/978-3-319-78999-6_7
Deutsch, C. V. (2021). Implementation of Geostatistical Algorithms. Mathematical Geosciences, 53(2), 227–237. https://doi.org/10.1007/s11004-020-09884-z
Dimitrakopoulos, R. (2018). Stochastic Mine Planning—Methods, Examples and Value in an Uncertain World. In: Dimitrakopoulos, R. (eds) Advances in Applied Strategic Mine Planning
Emery, X. (2015). Geoestadística. Ingenierìa de Minas, Universidad de Chile.
Rossi, M. E., & Deutsch, C. V. (2014). Mineral Resource Estimation. In Mineral Resource Estimation. Springer Netherlands. https://doi.org/10.1007/978-1-4020-5717-5