Las variables aditivas y no aditivas III: revisando propiedades de aditividad y linealidad de las concentraciones tipo %

Esta es la última entrada relacionada a las variables aditivas y las no aditivas. Recuerden que pueden encontrar sobre las variables no aditivas geotécnicas y metalúrgicas en nuestra entrada anterior.

¿Son aditivas y lineales la concentraciones de Cu (%)?

A continuación, revisaremos las variables de concentración del tipo % en masa definida por:

Concentración (X) % =100* (masa)_X/(masa)_Tot, esto es la cantidad en gramos del elemento de interés (X) con respecto de la masa total de la muestra ((masa)_Tot) multiplicado por 100 para obtener la concentración en %. La Tabla 1 presenta dos muestras para determinar su aditividad, se separa entres3 componentes para entender, posteriormente, el efecto de la densidad. La muestra M_01 pesa 100 gramos (ver fila b), con 1 gramo de Cu (ver fila a), 15 gramos de Mag y 84 gramos de ganga, obteniendo como resultado 1% de Cu (ver fila c) para la muestra M_02 se obtiene 2% de Cu. En la última columna se mezclan ambas muestras y aplicando la definición se obtiene una ley de 1.67 % de Cu.

Para demostrar su aditividad debemos obtener la misma ley de la mezcla de muestras M_01 y M_02 con la definición y=a₁x₁ + a₂x₂ +…+ a_nx_n, los pesos de a₁…a_n están dados por el denominador de la definición de ley, que es masa total, entonces tenemos que concentración de Cu de M_01 + M_02 es:

Cu% _{M_01 + M_02} =(100g_{M_01}/300g_{M_01_M_02}) *1%Cu_{M_01}+(200 g_{M_02}/300 g _{M_01_M_02}) *2%Cu _{M_02}=1.67

El valor obtenido es el mismo obtenido aplicando la definición de leyes en % y presentado en la Tabla 1 con la suma de las muestras M_01 y M_02. Por lo tanto, nos encontramos ante una variable aditiva, en particular, es aditiva en el espacio de la masa total de la definición de concentración (X) %.

Ahora, cuando utilizamos esta variable para realizar estimaciones espaciales, estas se realizan en el espacio euclidiano 3D (volumétrico) y es en este espacio, euclidiano o volumétrico, que se asume un comportamiento lineal de los datos para las ecuaciones de KO o simulaciones.

Como primer paso, vamos a revisar la concentración del X (Cu, por ejemplo) en el espacio de masa total y en el espacio volumétrico para entender como se relacionan o comportan estos valores.

Para simplificar la ley expresada entre 0 y 100% lo expresaremos en 0 y 1.

Concentración de (X) en el espacio de masa total:  (X) = (masa)_Cu/(masa)_Tot entonces:    

Concentración de (X) en el espacio de euclidiano:  (X) = (masa)_Cu/ (volumen)_Tot   = (masa)_Cu/ (masa/ρ)_Tot ,

donde (masa)_Cu = metal de interés,  /(masa)_Tot = masa total de la muestra, (volumen)_Tot = volumen total y (masa/ρ)_Tot  = masa total de la muestra dividido por la densidad de la muestra.

Con estas relaciones podemos transformar las concentraciones del espacio de masa total a concentraciones del espacio euclídeo.

Para el ejercicio, solo el denominador de la definición (la masa total de la muestra, (masa)_Tot) se reemplaza a partir de la definición de la densidad, porque la densidad de las distintas muestras es variable y dependerá de la composición de los minerales presentes. Por otro lado, el numerador no se reemplaza por la definición de la densidad porque la densidad es la misma en las distintas muestras, ya que el metal analizado es el mismo y, por ende, su densidad.

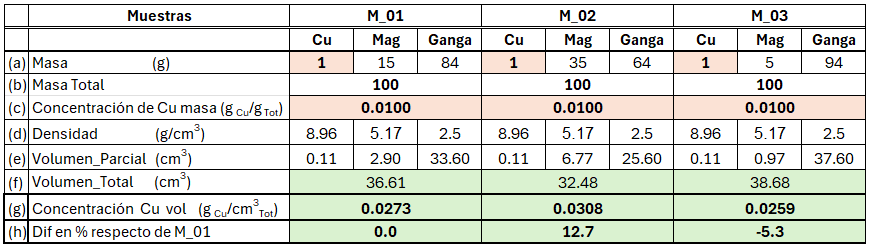
Para comenzar, transformaremos la ley de Cu de tres muestras (M_01, M_02 y M_03) para visualizarla. En la Tabla 2 se muestra que cada muestra contiene Cu, magnetita y ganga, junto con sus respectivas densidades (d) y masas (a). Las concentraciones se expresan como la razón entre las masas (c) dentro del espacio de masa total. A partir de las densidades de cada componente (e), convertimos las masas en volúmenes para obtener el volumen total (f), aplicando así la definición de concentración o ley volumétrica en el espacio euclídeo (volumétrico).

Si comparamos la concentración volumétrica de las muestras M_02 y M_03 con la de la muestra M_01, lo primero que se aprecia es que los volúmenes difieren entre ellas, al igual que sus concentraciones volumétricas (h). Así, mientras en el espacio de masa total las concentraciones son iguales para todas las muestras, en el espacio volumétrico estas mismas muestras exhiben concentraciones distintas debido al efecto de las diferentes densidades.

De este ejercicio se desprende que, al estimar concentraciones, la asunción de un comportamiento lineal impacta de manera distinta según el espacio en que se defina la variable de estimación. Cuando la linealidad se aplica a la variable definida en el espacio de masa total, se está exigiendo implícitamente que tanto la cantidad de Cu como la densidad de la muestra varíen de forma lineal de manera conjunta, algo difícil de justificar conceptualmente. En cambio, al asumir linealidad para la variable de concentración definida en el espacio volumétrico, lo que se pide es que el contenido de Cu se comporte linealmente en el espacio; esto sí es razonable, dado que tanto el espacio de estimación como la variable están definidos en un espacio volumétrico (euclídeo).

En el caso de la variable definida en el espacio de masa total, el contenido de Cu solo se conoce una vez que se estima la densidad, lo que implica que la cantidad final de Cu depende directamente de dicha estimación. Esto es relevante, porque no siempre se dedica la suficiente atención a la estimación de la densidad, pese a su impacto en el resultado.

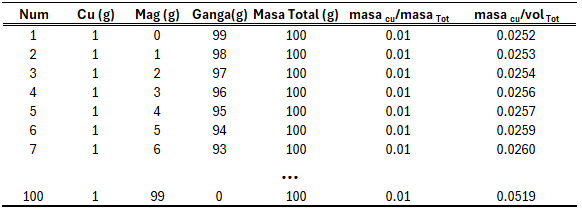
Para visualizar gráficamente la relación entre las variables de concentración definidas en el espacio de masa total y en el espacio volumétrico, se elaboró la Tabla 3 a partir de las definiciones previas. Esta tabla contiene 100 muestras cuya masa total es siempre de 100 g. Cada muestra está compuesta por Cu, magnetita (Mag) y ganga. El contenido de Cu es constante en todas las muestras (1 g), mientras que la cantidad de magnetita aumenta progresivamente de 0 g a 99 g, reduciéndose en la misma proporción la ganga.

Para cada muestra se calcula la concentración de Cu tanto en el espacio de masa total (masa Cu / masa total) como en el espacio volumétrico (masa Cu / volumen total).

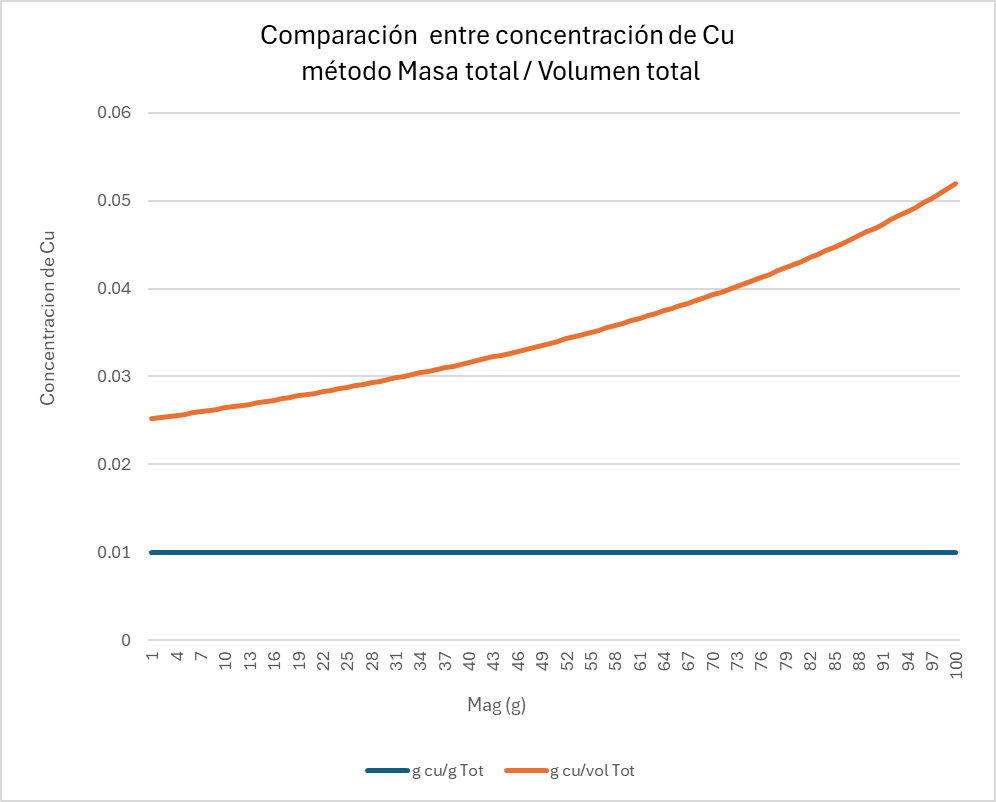
A partir de esta tabla se genera el gráfico presentado en la Figura 1. En él se observa que las definiciones de las variables en ambos espacios no presentan un comportamiento lineal. Mientras la variable definida en el espacio de masa total permanece constante, la concentración definida en el espacio volumétrico aumenta a medida que crece la densidad (producto del mayor contenido de magnetita). Además, el gráfico evidencia que la relación entre ambas variables tampoco es lineal.

En el gráfico siguiente (Figura 2), generado a partir de una tabla similar a la anterior pero compuesta únicamente por Cu y ganga, se incrementa progresivamente el contenido de Cu y se representan dos variables: la concentración de Cu definida en el espacio volumétrico y la definida en el espacio de masa total. El resultado muestra que la relación entre ambas variables es no lineal.

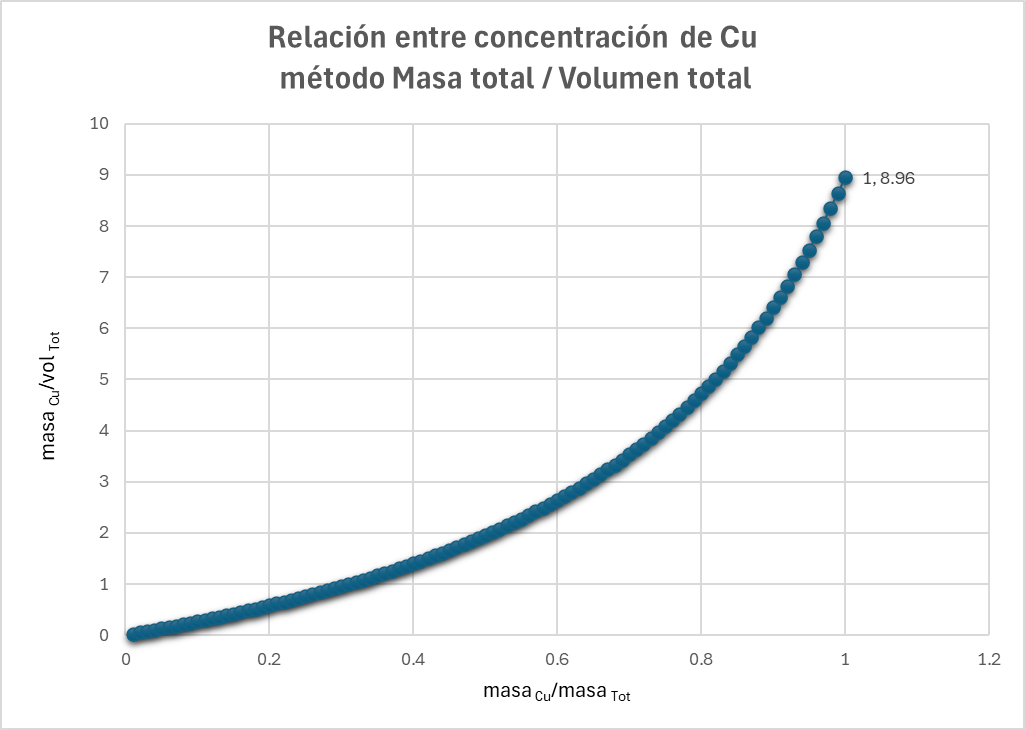
Como resumen, ambas variables son aditivas en sus respectivos espacios (espacio de masa total y espacio volumétrico). Para ambas, debemos asumir linealidad al estimar (ya sea mediante kriging o simulaciones). Sin embargo, en el caso de la concentración definida en el espacio de masa total, la concentración de Cu se relaciona de manera no lineal con el espacio euclídeo (volumétrico) de la estimación, debido a las variaciones de densidad entre las muestras. La relación entre ambos tipos de concentración se expresa como: concentración CuV = concentración CuM × (masaTot / volTot).

Esto plantea la pregunta: ¿cómo controlar este comportamiento no lineal del dato en el espacio euclídeo? Si la densidad fuera constante en las muestras, la no linealidad desaparecería. Por ello, una estrategia consiste en definir dominios adecuados que reduzcan la variabilidad de la densidad. En la misma línea, las muestras con densidades muy distintas pueden tratarse como outliers. Además, como corolario, se establece la importancia crítica de estimar correctamente la densidad, ya que esta determina la cantidad de Cu presente en el depósito.

Por último, aunque la variable de concentración volumétrica es plenamente compatible con el espacio de estimación y permite obtener directamente el contenido de Cu sin involucrar la densidad, presenta una desventaja práctica: medir el volumen total es muy difícil. Por esta razón, la variable que realmente se mide y se utiliza es la del espacio de masa total. Aun así, es altamente recomendable realizar los ejercicios comparativos entre ambas definiciones de concentración, ya que permiten comprender mejor las variables que utilizamos de forma habitual y, sobre todo, reconocer sus limitaciones con el fin de aplicar correctamente las definiciones, procedimientos, cálculos y estimaciones.

Con esto cerramos la serie sobre variables aditivas y no aditivas. Esperamos que haya sido de su interés y que les haya permitido profundizar en estos conceptos. Les invitamos a estar atentos a nuestras próximas publicaciones.