Las variables aditivas y no aditivas II: ejemplos de variables no aditivas geotécnicas y metalúrgicas

Siguiendo nuestra serie de entradas sobre variables aditivas y no aditivas, hoy hablaremos del caso de las geotécnicas y metalúrgicas. Recuerden que pueden encontrar las definiciones básicas y propiedades en nuestra entrada anterior.

Ejemplo de variables geotécnicas

En los siguientes ejemplos, no se pretende abordar la estimación de las variables no aditivas, sino revisar elementos básicos que permitan establecer un modelo conceptual coherente y una metodología de estimación que aborde adecuadamente el problema.

Previo a la definición de las variables geomecánicas, corresponde repasar los conceptos de roca intacta, discontinuidad y macizo rocoso. Las rocas se caracterizan en función de las propiedades del material que las constituye, tales como su comportamiento reológico (deformación de los materiales), su densidad, porosidad, etc.

La roca intacta corresponde exclusivamente al material ubicado entre las discontinuidades. Mientras que el macizo rocoso es el material que contiene las discontinuidades.

Para describir una zona, es necesario utilizar indicadores que den cuenta tanto de las propiedades de la roca intacta como del macizo rocoso. La Figura 1 presenta las variables de un macizo rocoso que están contenidas en la variable denominada Rock Mass Rating (RMR) desarrollada por Z.T. Bieniawski entre los años 1972 y 1973, actualizada posteriormente.

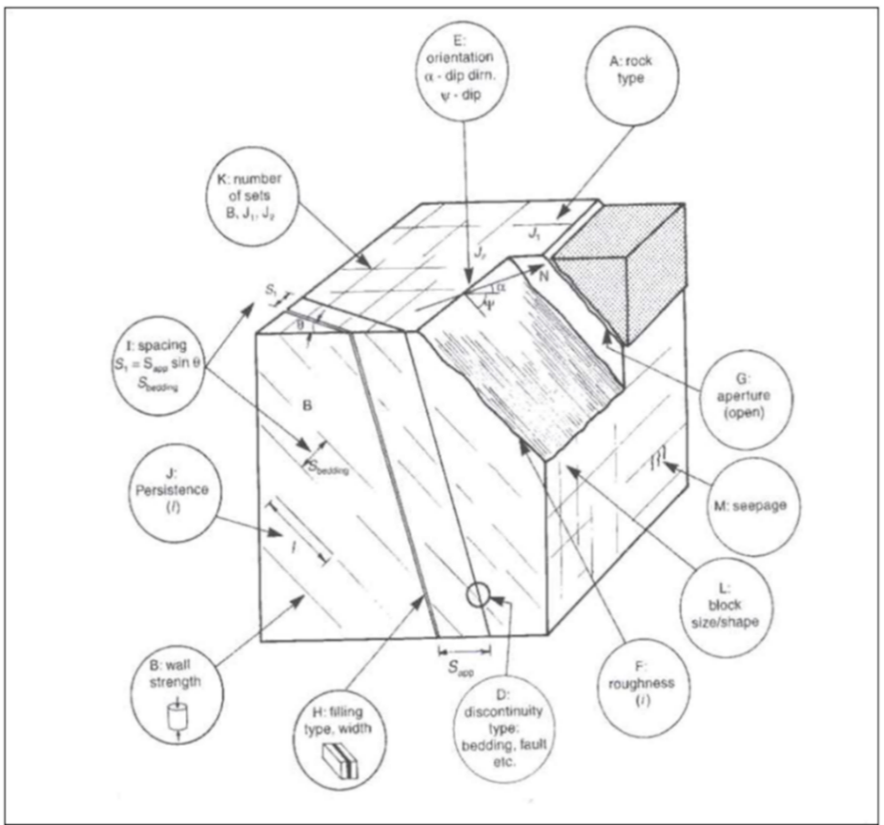
Variables no aditivas en geotecnia:

Entre las variables no aditivas en geotecnia se encuentran la resistencia al corte (que depende de la cohesión y del ángulo de fricción), el módulo de deformación (no lineal con tensiones aplicadas) y el coeficiente de permeabilidad (relacionado de forma logarítmica con el tamaño de los poros). Estas son variables que requieren transformación o modelado especial, como usar escalas logarítmicas, o que no se estiman directamente, sino que se estiman a partir de sus componentes aditivos. Otros ejemplos de este tipo de variables son: FF (Frecuencia de fractura), RQD (Rock Quality Designation), UCS (Uniaxial Compresive Strength), RMR (Rock Mass Rating), MRMR (Mining Rock Mass Rating), Q (Rock Tunneling Quality Index) y GSI (Geological Strength Index).

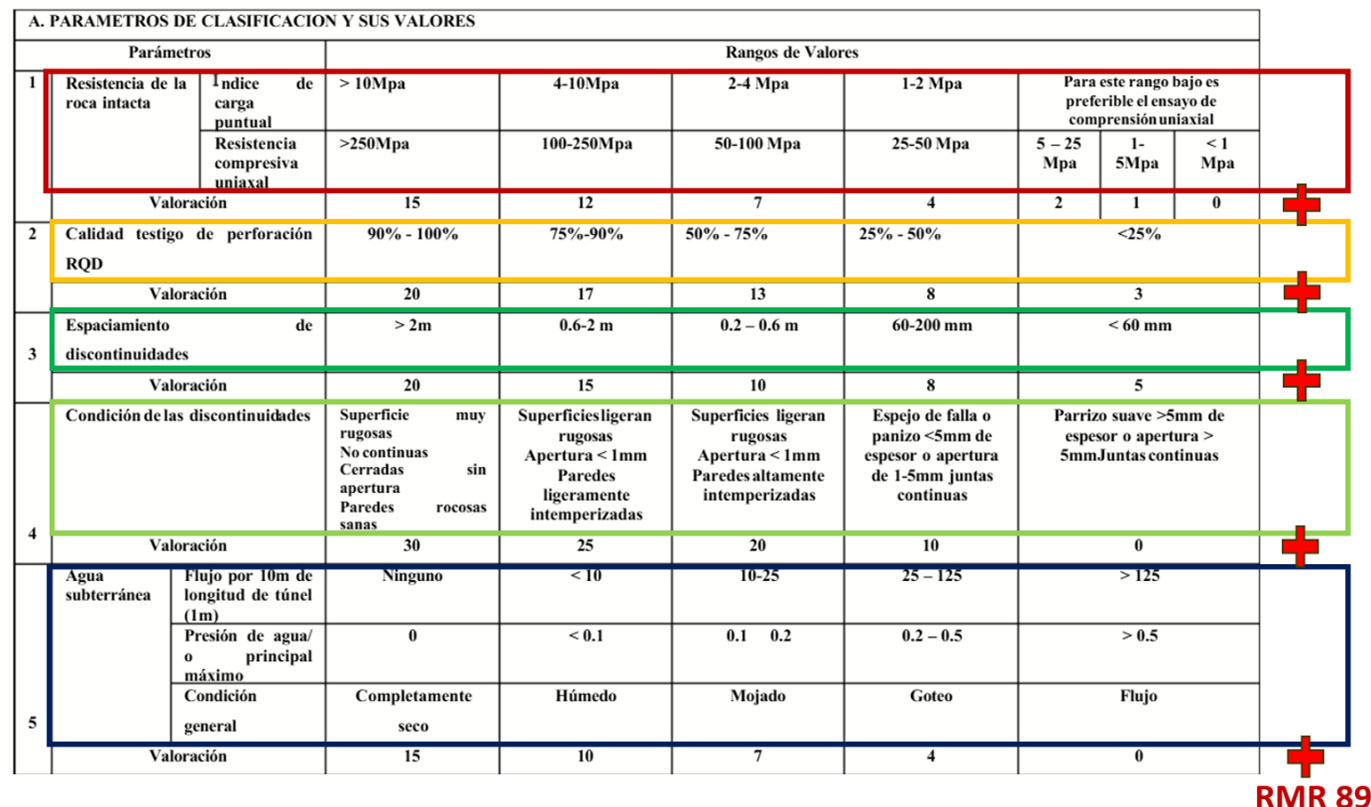
En la Tabla 1, se muestra la composición de la variable RMR, que corresponde a la sumatoria de variables parciales que permiten calcular la variable RMR; para ello, se suma la valoración de cada box coloreado. Por ejemplo, si el RQD de la muestra es 65 %, la valoración asignada es 13; se realiza este cálculo para cada una de las variables que componen el RMR. Si observamos la valoración asignada a cada tramo de la variable RQD, no se relaciona en forma lineal respecto de los valores medidos de esta variable, esto tiene como consecuencia que la variable RMR sea “no aditiva” y no lineal por lo que no se puede estimar directamente. La recomendación es estimar cada variable por separado y calcular posteriormente su valoración. Se debe considerar que variables como RQD, FF y resistencia de la roca intacta son variables direccionales por lo que no son aditivas, pero se pueden estimar bajo ciertas condiciones.

Variables direccionales:

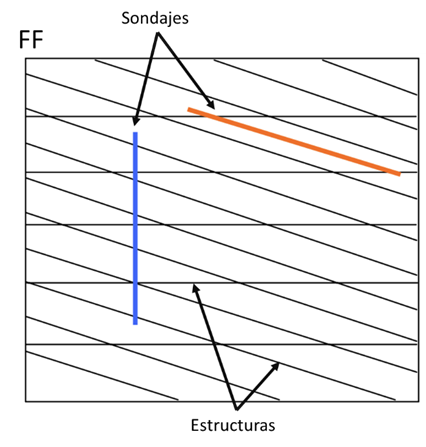
Cuando hablamos de variables direccionales, debemos entender que la orientación espacial en la que se mide la variable condicionará el valor de la muestra, es decir, depende de la dirección en que esta sea medida, como FF, RQD y resistencia a la compresión.

En la Figura 2 , las líneas rojas y azules representan soportes de un metro de largo; es fácil verificar que, en la dirección vertical (de color azul), FF = 9 [fracturas/m]; mientras que para el sondaje inclinado (de color rojo), FF = 2 [fracturas/m]. Este simple ejemplo muestra la enorme dependencia de la dirección que puede tener la variable.

Lo mismo ocurre con otras variables geotécnicas como el RQD. En el caso del RMR, depende, entre otras cosas, del espaciamiento entre discontinuidades y del RQD, ambas variables direccionales. Para estimar estas variables podemos establecer que el valor utilizado será el de menor calidad de modo que los valores a estimar sean la peor condición, y que esta condición se refleje en el valor del RMR, también ayuda el establecer dominios con baja varianza de los datos. Tenemos que considerar que rocas con mayor plasticidad, como tobas, o que presenten alto contenido de arcillas por alteración, presentarán menor cantidad de estructuras que rocas sometidas al mismo esfuerzo, pero más rígidas, como basaltos sin alterar. En resumen, establecer dominios geológicos ayuda a enfrentar la estimación de variables no aditivas.

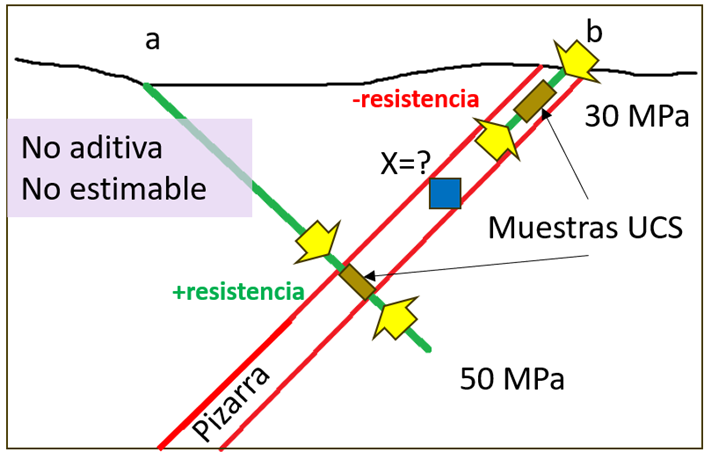
Otro caso es la variable resistencia de la roca intacta, al medir, por ejemplo, la variable UCS (Uniaxial Compressive Strength) en una roca metamórfica (pizarra) como muestra la Figura 3, por el hecho de ser medidos en diferentes direcciones, sus valores serán diferentes, debido a que las medidas realizadas paralelas al eje máximo de deformación son más bajas que las realizadas perpendiculares a estas. Esta variable presenta variaciones direccionales que están relacionadas con los elipsoides de deformación en las rocas metamórficas, pero si las medidas son realizadas en rocas intrusivas, podemos asumir un comportamiento isotrópico, además de asumir aditividad en los diferentes dominios litológicos; por lo tanto, podemos realizar estimaciones de estas variables en cada dominio. El contexto geológico permite simplificar el problema de este tipo de variables.

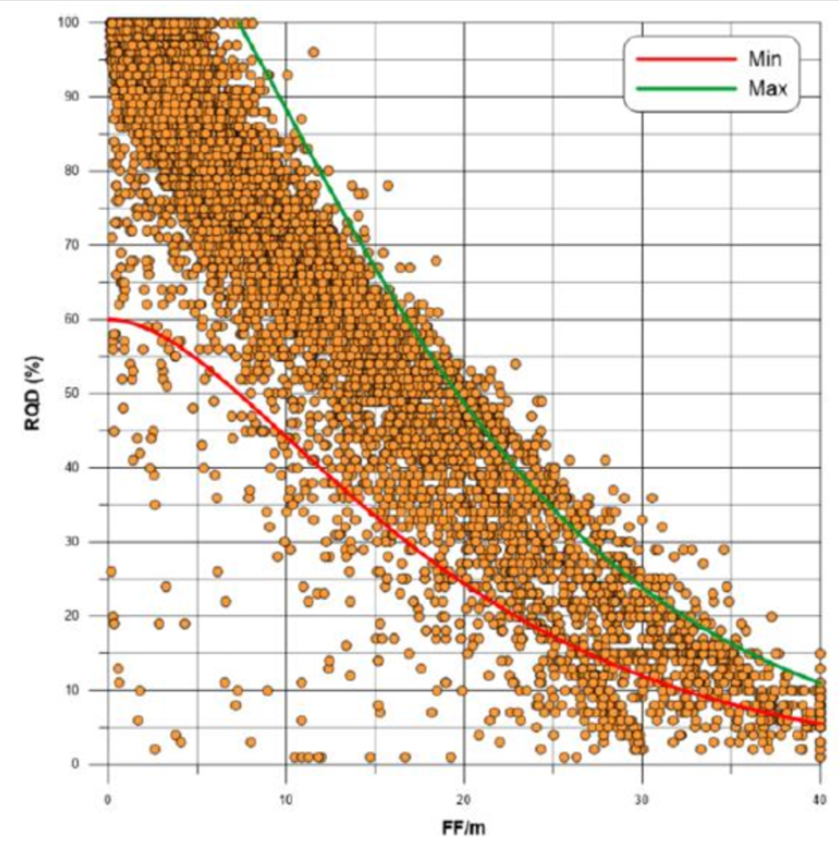
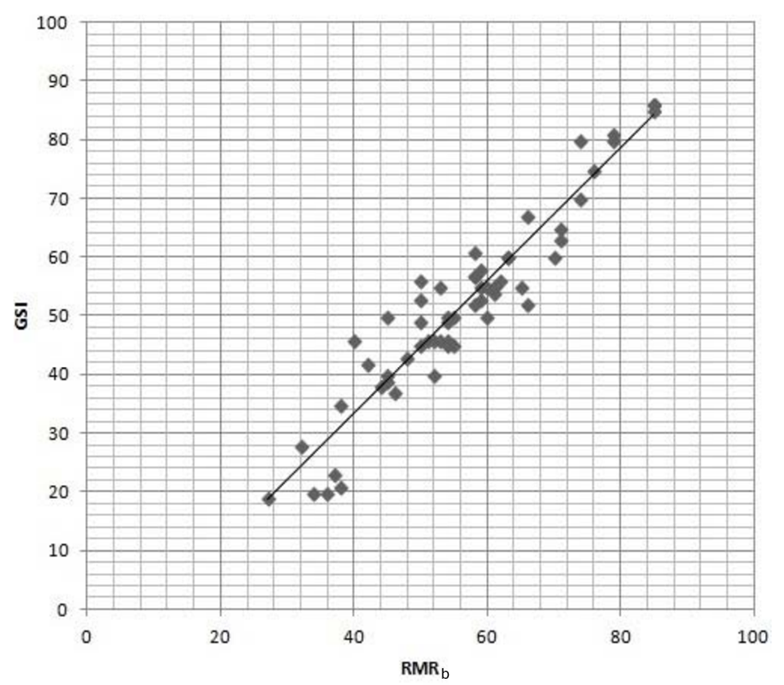
Otra propiedad importante de las variables geotécnicas es la correlación que existe entre estas. Por un lado, estas correlaciones que presentan los datos también deben observarse en el modelo estimado pudiendo utilizarse como una de las validaciones de las estimaciones realizadas (ver Figura 4 y Figura 5). Por otro lado, estas mismas relaciones de las variables pueden ser usadas en la estimación, por ejemplo, el método de los residuales, que permite conservar tanto la correlación entre variables como conservar su variabilidad.

Ejemplo de variables metalúrgicas

Ahora analizaremos la variable de respuesta Work Index (Wi), definida como el índice de trabajo que requiere la potencia necesaria para moler un material desde un tamaño teóricamente infinito hasta uno tal que pase el 80% de los 100 micrones, permitiendo así obtener una buena estimación de la energía necesaria para la molienda (kWh/tc). Para calcular el índice Wi, deben obtenerse datos experimentales bajo estrictas condiciones de operación.

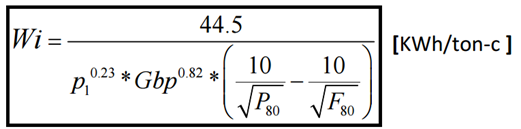
Cálculo para obtener el Wi para molino de bolas donde:

P₈₀ [µ𝑚] es el tamaño de tamiz que deja pasar el 80% del producto final.

F₈₀ [µ𝑚] es el tamaño de tamiz que deja pasar el 80% del material de alimentación.

Gbp [𝑔/𝑟𝑒𝑣] se refiere a los gramos por revolución; corresponde al índice de moliendabilidad (grindability) del molino de bolas y es una variable de respuesta de un ensayo.

p₁ [µ𝑚] corresponde a la abertura de la malla de corte utilizada para cerrar el circuito (tamaño 100% pasante del producto).

Yan & Eaton (2003) estudiaron el comportamiento del índice de Bond en mezclas físicas de mineral de alta (Wi = 14.0 kWh/t) y baja competencia (Wi = 6.0 kWh/t). Consideraron que la mezcla debería corresponder al promedio aritmético de los valores ingresados (Wi = 10.0 kWh/t). Sin embargo, la mezcla física probada en laboratorio arrojó un valor de 12,23 kWh/t (Figura 6).

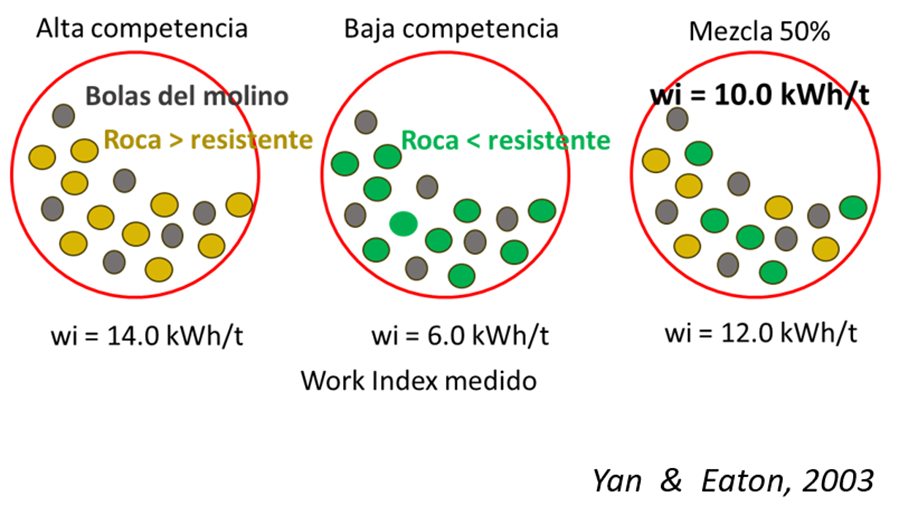
Esta diferencia se debe a la definición de la variable, al ser una función de respuesta (ensayo) a un tratamiento (kWh/t) no considera variables internas de las muestras ni del sistema por lo que no da respuesta a todas las condiciones de mezclas, como la señalada anteriormente donde el material blando actúa como amortiguador del material más resistente permaneciendo mayor tiempo en el molino para alcanzar el tamaño deseado.

Una forma de enfrentar este tipo de variables es agrupar la data en dominios con baja dispersión, de modo que se evite la mezcla de materiales de muy diferentes competencias. Como de todos modos el material se va a mezclar en la planta, se pueden ensayar las distintas proporciones de mezclas y asignar los valores a partir de una regresión u otro método a los bloques que presenten rangos de mezclas.

De este ejemplo se desprende la necesidad de conocer el comportamiento de las variables de respuesta al mezclar muestras con características distintas (ensayos). En este ejemplo, en la fórmula no se indica el contenido de arcillas como variable (que pudiera modificar el resultado), y es precisamente este mineral el que en ciertas condiciones genera una respuesta no esperada del ensayo. Por ello, es importante conocer el ensayo y el yacimiento para revisar qué condiciones son modificables y testearlas.

En el siguiente blog, se presentará la variable de concentración de Cu en %. Se revisarán sus propiedades y características de modo que podamos entender este tipo de variables y qué consideraciones debemos considerar a la hora de estimar.