Las variables aditivas y no aditivas I: definiciones y propiedades

Al realizar una estimación o simulación de una nueva variable es importante preguntarnos por la propiedad aditiva de esta, su propiedad lineal y conocer su definición. Si la variable no es aditiva, este conocimiento permite evaluar metodología y técnicas para estimarlas, realizando, por ejemplo: simplificaciones, acudiendo a la definición para estimar las variables que la definen o aplicando dominios donde esta se comporte aproximadamente lineal.

Conocer las variables permite establecer sus propiedades matemáticas, por ejemplo, asumir su linealidad o propiedades geológicas para adoptar criterios válidos que permitan conceptualizar su comportamiento (ejemplo establecer que la variable tiene distintos comportamientos de acuerdo con condiciones geoquímicas, geofísicas) este conocimiento nos permite finalmente extrapolar los valores en el espacio y/o tiempo.  

Pero ¿cómo se define una variable aditiva? ¿cómo se distingue una variable aditiva de una no aditiva? ¿Cuáles son sus características? ¿Cómo abordamos la estimación de variables no aditivas?

Partamos con la definición y propiedades de las variables para comprender y discriminar las variables aditivas de las no aditivas:

Primero, una variable aditiva es aquella que en la unión de sus partes corresponde a la suma de estas, por ejemplo: largo (m), área (m²), volumen (m³), tonelaje (masa). Por ejemplo: 2(m³) + 3 (m³) = 5 (m³).

Segundo, veamos los conceptos de propiedades extensivas e intensivas de las variables. Una propiedad es extensiva cuando esta depende del tamaño, cantidad o extensión del sistema. Estas variables son aditivas, como la masa y el volumen; si se combinan dos muestras, las propiedades extensivas se suman. Por ejemplo, si se tienen dos objetos con masas de 2 kg y 3 kg, la masa total será 5 kg. Por otro lado, una propiedad es intensiva cuando esta no depende del tamaño, cantidad o extensión del sistema. Las propiedades intensivas; como la densidad, la temperatura y la presión, no se suman cuando se combinan diferentes sistemas. Por ejemplo, si se tiene un litro de agua con una densidad de 1 g/cm³ y agregas otro litro de agua con la misma densidad, la densidad total del sistema sigue siendo 1 g/cm³ (no 2 g/cm³). Con este ejemplo de la densidad podemos establecer que no es una variable aditiva sensu stricto, porque su suma no es 2 g/cm³.

Para incorporar estas variables intensivas, como la densidad, a aditivas, debemos ampliar la definición de aditividad, para ello incorporaremos la definición de funciones lineales.

Tercero, estableceremos un dominio (x,y) e incorporaremos la siguiente función y=3x+2 en un gráfico de coordenadas (x,y), como ya sabemos, esta función corresponde a una línea recta. Luego, podemos generalizar y=a₁x₁ + a₂x₂ +…+ a_nx_n  y donde a₁ + a₂ +...+ a_n=1, son los pesos asignados a cada muestra a₁…a_n y deben ser asignados en función del denominador de la definición de la variable. Para el caso de la densidad (ρ=m/V), usaremos el volumen para determinar el peso “a” de su fusión lineal.

Ahora, debemos detallar la asignación de los pesos (a₁…a_n). Como ejemplo, usaremos la definición de densidad ρ=m/V = gr/cm³; la ponderación se realiza por el denominador, en este caso, volumen, ya que el denominador define el espacio matemático en el que se define la variable. En el siguiente ejemplo, usaremos tres muestras con volúmenes variables y masas distintas. A continuación, mezclamos estas muestras y calculamos su densidad en un laboratorio (esto es importante porque en las variables no aditivas el cálculo de la mezcla no se expresa materialmente, esto es al mezclar dos muestras con valores diferentes el valor obtenido a partir del cálculo no se condice con el valor obtenido en laboratorio, más adelante se revisará este efecto con la variable Work Index), para ello sumamos el total de las masas de las muestras y el total del volumen (medición de laboratorio), el valor se encuentra en (a) de la Tabla 1, que es la densidad real.

Para obtener la densidad total, aplicamos: Densidad =a₁*D₁ + a₂*D₂+ a₃*D₃, donde a_i corresponde a los pesos calculados con los siguientes métodos:

1. Media aritmética (b), donde los pesos se calculan como a_i=1/n, donde n es el número de muestras. Pero el resultado en (b) es distinto al obtenido en (a), por lo que este método no es aplicable.
2. Sumar las densidades de las muestras con los pesos obtenidos al ponderar las masas de las muestras, a_i=M_i /M_T, donde M_i son las masas de las muestras y la M_T masa total muestras. Pero el resultado (c) no concuerda con el valor de (a), por lo que este método no es aplicable.
3. Sumar las densidades de las muestras con pesos obtenidos al ponderar los volúmenes de las muestras, a_i= V_i /V_T , donde V_i son los volúmenes de las muestras y V_T es el total del volumen. En este caso (d)=(a).

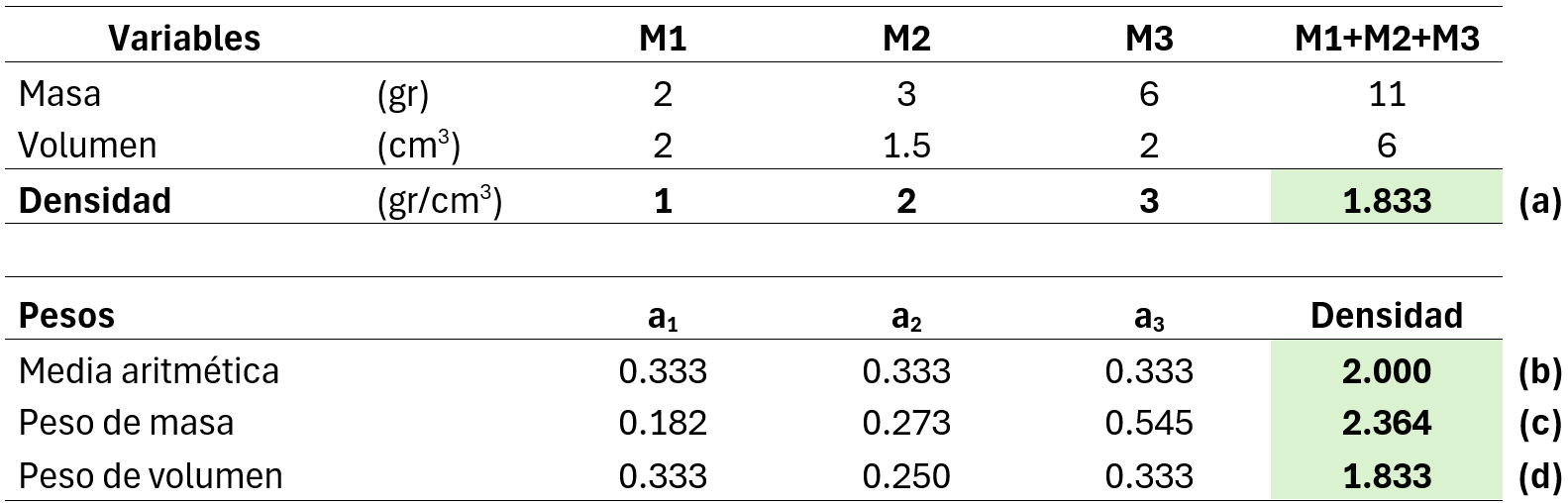
Esto nos indica que la unidad en la que se mide el valor de la variable se encuentra en el denominador, por tanto, para promediar la variable debemos considerar el denominador para obtener el valor de la variable en la mezcla.

Con esto, estamos listos para generalizar la aditividad de las variables: una variable será aditiva si la suma de sus partes permite obtener el valor del total, tal que, y=a₁x₁ + a₂x₂ +…+ a_nx_n, donde se cumplen las siguientes restricciones, si tenemos una variable extensiva se cumple a₁ = a₂ = a_n=1 y si es una variable intensiva a₁ + a₂ +...+ a_n   =1.

Otras propiedades

Ya mencionamos que la propiedad de linealidad nos permite calcular la mezcla total, a partir de las muestras individuales, y también nos permite determinar la aditividad o no de una variable, calculando la mezcla y contrastando con la observación en laboratorio. Las funciones lineales presentan el principio de superposición, lo que establece que la respuesta total de la muestra es la suma de las respuestas individuales de cada submuestra (recordar que no estamos estimando, estamos calculando una mezcla de distintas muestras).

Esta linealidad también es aplicable a variables cuyo origen se genera a partir de una función basada en otras variables, para que una variable generada a partir de una función sea aditiva, entonces la función debe ser lineal (hasta ahora hemos asumido que las variables de origen son aditivas). Si una variable no se puede obtener mediante una suma o promedio directo ponderado, entonces estamos ante una variable no aditiva. Algunos ejemplos de variables no aditivas son las generadas con funciones de dependencia logarítmicas, exponenciales, etc.

Las variables no aditivas son aquellas cuyo valor de la media no se puede obtener mediante una suma o promedio directo ponderado porque tienen un comportamiento no aditivo (no lineal). Un ejemplo de esto son las variables como resistencia y permeabilidad, donde su media no representa fielmente la realidad física.

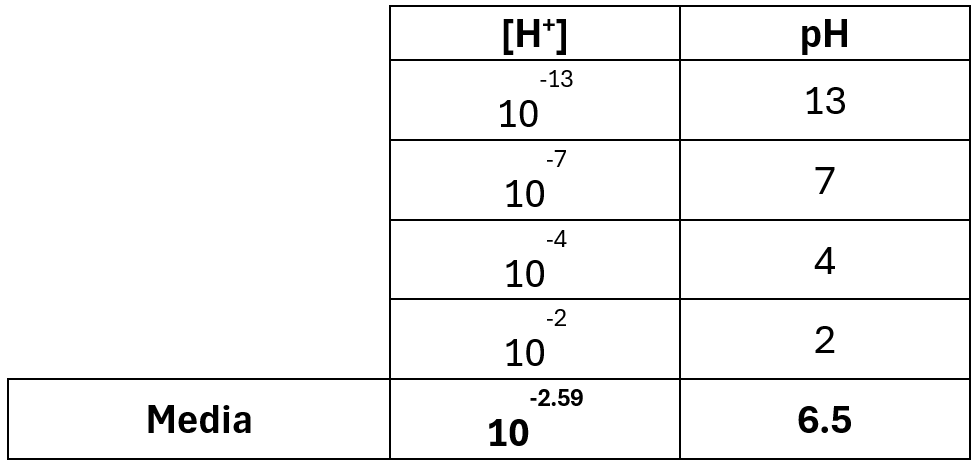
Veamos este concepto con el ejemplo de la variable pH. En la Tabla 2, se encuentra la variable pH, que se define como pH=-Log₁₀[H⁺], si obtenemos la media directamente de la definición de pH el resultado es 6.5, sin embargo, si lo obtenemos a partir de la concentración el pH es 2.59. Este ejemplo nos muestra que no se puede obtener promedios a partir de funciones no lineales, por lo que se debe acudir a las definiciones para obtener los resultados correctos. En particular, aquí el promedio ponderado lo obtenemos directamente de la concentración transformando luego la concentración a pH.

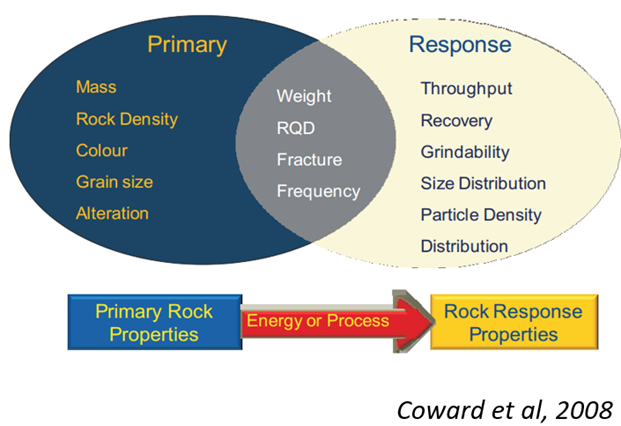
Existen otras propiedades de las variables en áreas como geotecnia o metalurgia que se pueden clasificar como primaria o de respuesta. Se entiende como propiedad primaria si representa una característica intrínseca del material de estudio y propiedad de respuesta si representa una característica de respuesta del material de estudio a algún proceso. Entre ambas clasificaciones se encuentran propiedades intermedias (ver Figura 1).

Las variables de respuesta son aquellas que corresponden al resultado medido dentro de un ensayo, que puede ser influenciado por factores que no se encuentran en la definición de la variable. En general, las variables de respuestas se consideran complejas y no-lineales.

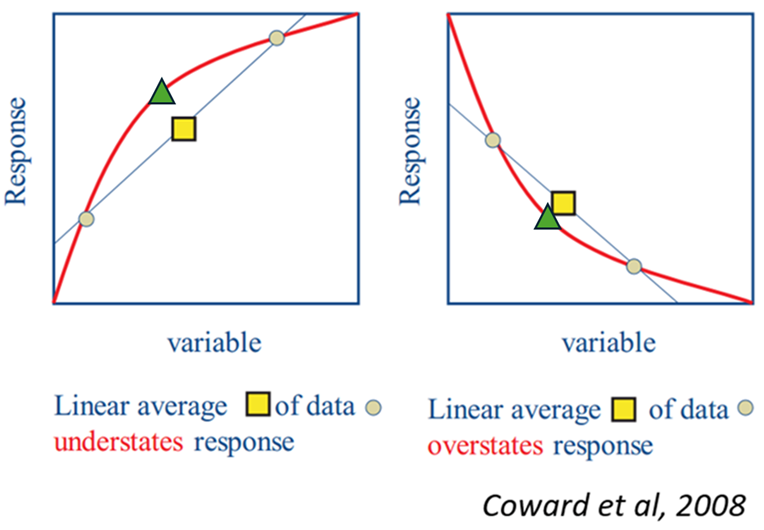
En la Figura 2, se muestra el efecto de calcular la variable de respuesta (cuadrado) a partir de dos muestras (círculos) como no es lineal, el resultado de calcular la mezcla de ambas muestras no se condice con la respuesta de esta (triángulo). Más adelante, revisaremos este problema con la variable work index.

Linealidad en las funciones de estimación

Un área relacionada con la aditividad de las variables es la geoestadística, esta es la rama de la estadística que analiza y modela la variabilidad espacial de fenómenos y se enfoca en la dependencia espacial de los datos, es decir, cómo la ubicación de una medición afecta a otras en su entorno. A diferencia de la estadística clásica, que considera datos independientes del espacio, la geoestadística estudia fenómenos regionalizados (esto es, el comportamiento de las variables en un volumen determinado).

Gran parte de los métodos realizados mediante geoestadística implican realizar medias aritméticas ponderadas y dependientes del espacio. A diferencia de la aditividad revisada anteriormente que se relaciona con la mezcla de muestras y el valor que toma en función de las muestras iniciales y en el espacio matemático definida en la variable.

A continuación, revisaremos la ecuación de kriging y de simulación para entender la relación con las variables aditivas.

El caso general de la función de estimación es:

Z(r)=b₁*Z(r₁) + b₂* Z(r₂) +...+ b_n* Z(r_n) 

Lo importante en la estimación es que los pesos (b₁… bn) están relacionados tanto con los valores de las variables como con sus relaciones espaciales, lo que se establece con su comportamiento variográfico.

Para el caso de ecuación kriging ordinario, se define como sigue:

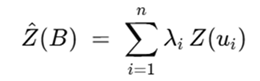
Y en el caso de la ecuación general de simulación condicional, como:

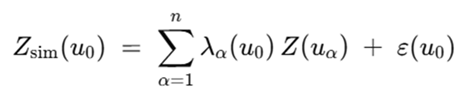
Ambas funciones son lineales, por lo que se requiere que las variables de entrada sean aditivas y, por lo tanto, lineales. Ahí radica la importancia de la aditividad y linealidad de las variables a estimar. La linealidad que requiere la estimación está definida en un espacio tridimensional. Para el ejemplo revisado de la densidad, la aditividad está definida también en el espacio (volumen) y la estimación de esta variable que también requiere linealidad en el espacio cumple completamente con los requisitos para su estimación.

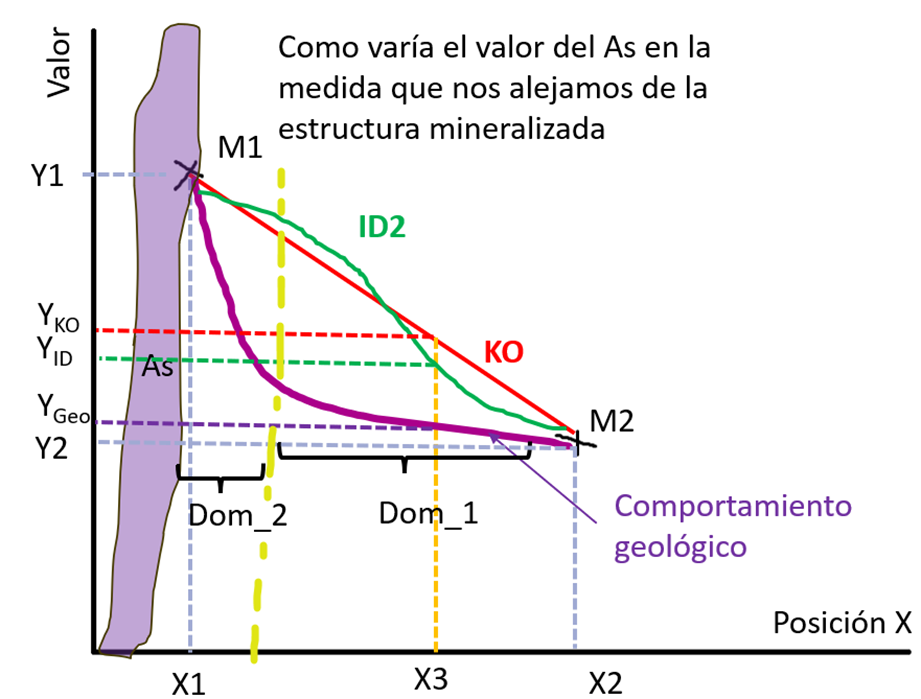
Ahora vamos a revisar el comportamiento espacial de una variable ubicada en diferentes dominios. En el siguiente ejemplo, se muestra cómo se comporta el arsénico (As) cuando nos alejamos de una veta mineralizada de enargita (Cu₃AsS₄), tenemos dos muestras (M1 y M2) con As y queremos determinar la ley (Y) en X3 (Figura 3). En la recta roja, se encuentra la estimación de kriging ordinario (KO) que es una función lineal; en verde, está la estimación del inverso de la distancia al cuadrado (ID2) que es una función no lineal; y la línea morada es el comportamiento real del arsénico.

Con base en este ejemplo, podemos establecer que para usar modelos lineales de interpolación (en variables de comportamiento no lineal) se requiere separar en este caso, a lo menos dos dominios entre X1 y X2 para que la variable se comporte aproximadamente lineal en sus respectivos dominios. Esto debido a que el comportamiento de esta variable no es lineal en estas condiciones (contacto de dique mineralizado con roca caja). Con este ejemplo se muestra la linealidad de la función de KO, la no linealidad de la función ID2 y, por otro lado, la no linealidad del comportamiento de una variable, pero al restringir los dominios podemos asumir un comportamiento aproximadamente lineal para aplicar métodos de estimación.

En el siguiente blog, se presentará un ejemplo de variable geotécnica y otro de variable metalúrgica para entender este tipo de variables no aditivas, sus definiciones, comportamiento y cómo enfocar la estimación con las restricciones propias de las variables.